LLM Training Optimization: Megatron and Deepspeed
References
LLM Training Optimization
There has been numerous attempts at optimizing LLM training due to the model size increasing, with memory being the bottleneck. Megatron-LM attempts to solve this problem by leveraging tensor parallelism (row-wise and column-wise parallelism). DeepSpeed focuses on minimizing memory utilization by splitting the memory used by the parameters (weights), gradients, and optimizer states (e.g. Adam optimizer) across GPUs. While this all sounds great, this puts a lot of pressure on the limited network bandwidth. I note some network specific aspects mentioned in the respective papers below:
Megatron-LM (NVidia’s Attempt)
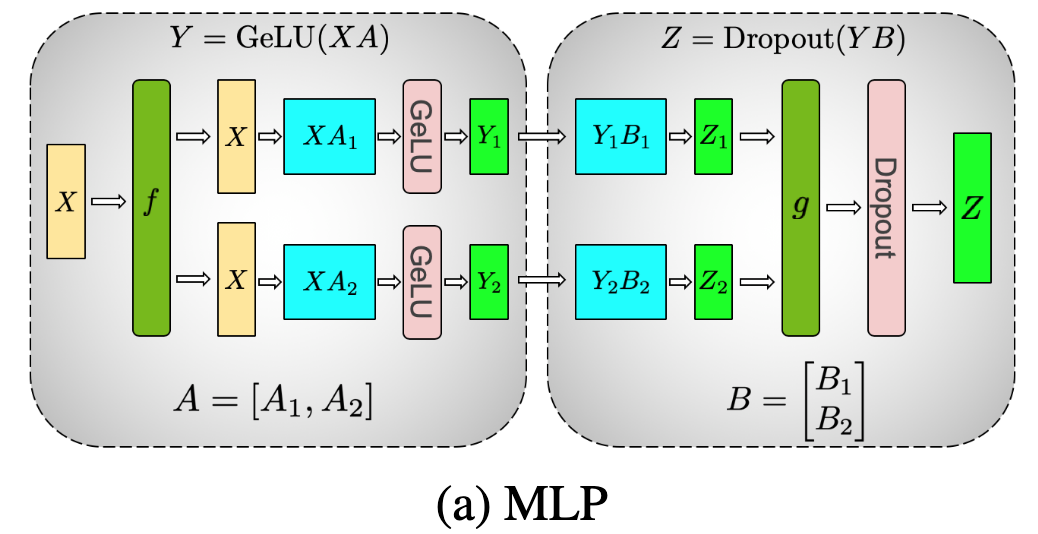

The self-attention block and MLP block within a transformer is split across GPUs (e.g. model parallelism) such that each GPU has a shard of a tensor. The tensor can be split column-wise or row-wise depending on the linearity of computation. In Megatron-LM we first have column-wise operations followed by row-wise operations that can be done in parallel across GPUs.
In the forward-pass, after column-wise parallelism and row-wise parallelism, g (ALL-REDUCE) is needed to ensure all GPUs have the same tensors before starting the next block. The f block is an identity function.
In the backward pass, the g block is now the identity function that replicates calculated weight gradients from previous blocks across GPUs. After gradient calculations, the f block is now an ALL-REDUCE collective.
This ALL-REDUCE is done within the Tensor Parallel communication group (within a server node) that is usually connected with high bandwidth links (~300 GB/s). Because we have a pair of ALL-REDUCEs per pass of a Transformer block, it is important to have high bandwidth links within a server when using Megatron.
Usually, Megatron is done in hybrid parallelism (TP + DP). If we have a 8 GPUs, a TP degree of 4, then we would have a DP degree of 2. The model is replicated across the two sets of GPUs:
Model Sharded (TP)
Model (Replicated) - [0, 1, 2, 3] --> use mini-batch A
Model (Replicated) - [4, 5, 6, 7] --> use mini-batch B
After a full forward pass, the activation tensors must be gathered through ALL-GATHER across DP groups. After the backward pass, the weights must be synchronized as the two collective groups use different mini-batches. This is usually done using ALL-REDUCE but Megatron can use the distributed optimizer which uses REDUCE-SCATTER within the data-parallel group to reduce gradient communication and shard optimizer states, further saving memory.
ZeRO (Microsoft’s Attempt)
The main focus of DeepSpeed is to minimize memory redundancies by sharding memory states across GPUs. The paper claims that while some models claim to be a certain size, additional allocations due to optimizers, gradients, activation, and transient buffers create a lot of OOM problems. This causes hardware to be the limit of what kind of models we can train.
DeepSpeed categorizes different memory uses as model states and residual states depending on how large/persistent the memory is.
Memory states: Memory allocation related to optimizer states, gradient, and parameters. I was surprised by the amount of data needed by the optimizer (e.g. Adam optimizer): time averaged momentum and variance of gradients to compute the updates. This takes up the majority of memory and is also kept in fp32. Gradient and parameter tensors are stored as fp16. When $\Psi$ is the total number of parameters, the Adam optimizer would need 4$\Psi$ amount of memory (each of the fp32 copies of parameters, momentum, and variance need this amount) while the gradients and parameters would each need 2$\Psi$ amount of memory.
Residual States: Memory allocations related to activations and temporary buffers. While activation checkpointing (store activations of some layers only, checkpoint them, and re-calculate when needed for gradient calculations) helps, the paper claims that activation memory still grows quite large for bigger models (a GPT-like model with 100 billion parameters requires around 60 GB of memory for batch size 32). The paper also mentions importance of memory management during training to prevent OOM due to memory fragmentation (there’s enough space but not contiguous due to frequent allocation-free).
I think the video above explains the concepts the best. Courtesy to the Microsoft Blog that made the video and explained the paper’s concepts clearly:
ZeRO (Zero Redundancy Optimization) is composed of 3 different types of optimizations:
Pos - Optimizer State Partitioning: Optimizer states are sharded by the number of GPUs (N). This means that each data parallel process needs to store and update 1/N of the total optimizer states. At the end of each training step, an all-gather is done across data parallel processes.
Pg - Gradient Partitioning: Gradients are sharded by the number of GPUs (N). Because each GPU only needs to process gradients they are responsible for and scatter them to other processes (reduce-scatter).
Pp - Parameter State Partitioning: When the parameters outside of its partition are required for forward and backward propagation, they are received from the appropriate data parallel process through broadcast. The paper claims that this results in 50% more communication than the baseline.
During forward pass, data parallel process responsible for a specific partition must broadcast the weights to all the data parallel processes. Once the pass is done, the parameters are discarded (because these are updated the next pass anyways). The total communication is therefore: $(\Psi \times N_d)/N_d$ , because it spreads the all-gather across the entire forward propagation. This is done one more time for the backward pass. “The total communication volume is therefore the sum of the communication volumes incurred by these all-gathers in addition to the communication volume incurred by the reducescatter of the gradients.” This gives a total communication volume of 3 $\Psi$.
ZeRO-R (for residual states) also has more communication overhead than the baseline model using MP. However, the increase is said to be only a tenth of the baseline:
Note that the message size is denoted as message_size = batch_size * sequence_length * hidden_size
Assuming we are using activation checkpointing, we would need two ALL-REDUCE in the forward pass, two ALL-REDUCE for the backward pass, and two ALL-REDUCE for activation checkpointing. Because the volume of a ALL-REDUCE is 2 * message size, we can say that the total volume is 12 message size.
However, for ZeRO-R, an additional ALL-GATHER is required before the forward recomputation of the back-propagation on each activation checkpoint. The paper states that “we checkpoint the input activation for each transformer block, requiring one all-gather per transformer block. The communication overhead Pa is therefore seq length ∗ hidden dim, since the communication volume of an all-gather is message size.”
