Study on LLM Inference Communication
References
Recap of LLM Inference (Transformer-based)
The LLM inference process is largely split into two: the prefill phase and decode phase. The prefill phase initializes the KV Cache by processing the user’s input (note that the user input’s length is unknown). The decode phase is responsible for providing the next tokens using a transformer block which consists of multiple attention layers and a feed-forward layer (MLP). New token information is appended to the KV Cache (and updating other token values), and the MLP generates the next token until the EOS is generated.
The prefill stage is compute bound but can process the input prompt in parallel, but the decoding phase is sequential (token by token) and the performance is memory bound.
Where does Communication Happen?
Similar to LLM training, LLM inference can also benefit from parallelization strategies such as TP and MP.
Little Bit of Background
About MLP Down/Up-Projections:
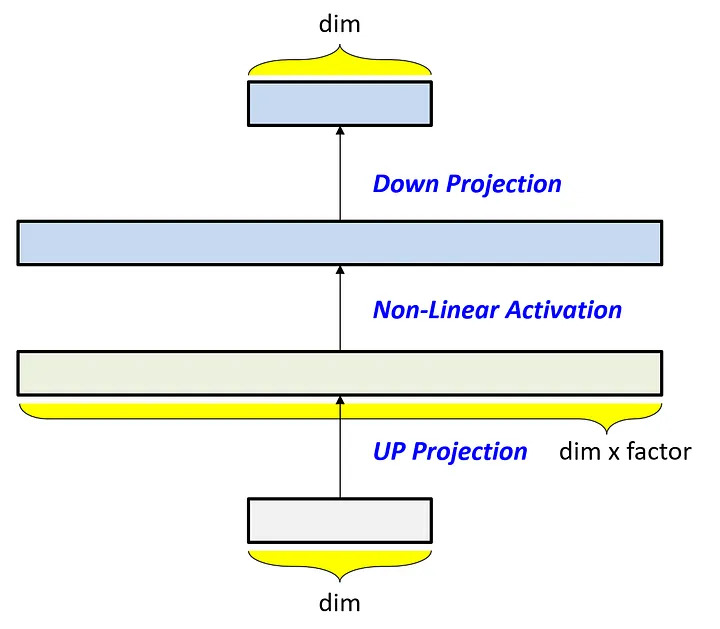
In LLM architecture, up-scaling and down-scaling are done because 1) the model better predicts next tokens at higher input dimensions (more information to play with) and 2) non-linear transformations are strengthened at higher dimensions. This is then scaled down to the original input dimensions as shown in the image above.
About Attention Output Projection: The attention output projection is the final linear layer within the multi-head attention mechanism. Its job is to combine the outputs from all the different attention “heads.”
Looking at this, you can kind of see how communication would be required in these two particular steps for tensor parallelism:
Tensor Parallelism (TP)
\[V_{tp}=(2L+1)\times(S_p+S_d-1)\times h \times b \times 2\left(\frac{t-1}{t}\right)+S_d\times \frac{v}{t}\times b\]The paper claims that the total volume of communication needed can be represented by the equation above. Let’s try understanding the equation.
- \((2L+1)\): Total number of all-reduce occurring ($2\times number\ of\ transformer\ layers$)
- \((S_p+S_d-1)\): Total sequence length (pre-fill and decode stage)
- \(h\) : the sequence length is processed by h different layers in MLP and this must be synchronized in tensor-parallelism
- \(b\) : bytes per element (float or double)
The terms following \((2L+1)\times(S_p+S_d-1)\times h \times b\) are the correction factor and the Gather operations for vocabulary projection respectively.
Pipelined Parallelism (PP)
\[V_{PP}=(p-1)\times(S_p+S_d-1)\times h \times b \times 2\]Pipelined parallelism is easier to understand because each node can process in parallel only if it is responsible for a pre-fill stage and can process sequentially only if it is responsible for the decode stage.
- The pre-fill stage takes \(S_p\times h \times b\)
- The decode stage takes \(h \times b\) because each token must be processed sequentially. There are a total of \(S_d\) of such tokens to process.
- The factor of 2 is to consider the fact that we must produce the same communication volume for both K and V matrices.
